Recurrence Relation and Time Complexity of Recursive Functions

Introduction

It can be challenging to determine a recursive function's time complexity when considering recursive functions using the same formula we used to get an iterative process. As a result, We must look for alternative solutions to this problem. Here is where the recurrence relation comes into play. Let's start by asking what the recurrence relation implies. A recurrence relation in mathematics is an equation that states that the nth term in a series of integers equals some combination of the terms that came before it. So any functions with recursion will have a recurrence relation, confused? To gain a thorough understanding, we must first be aware of all possible ways that can solve recurrence relations.

• Substitution Method
• Recursive Tree Approach
• Masters Theorem

So, in this article, we will first look at the substitution technique, and then move on to other topics in subsequent articles.

Problem

Consider a recurrence relation,

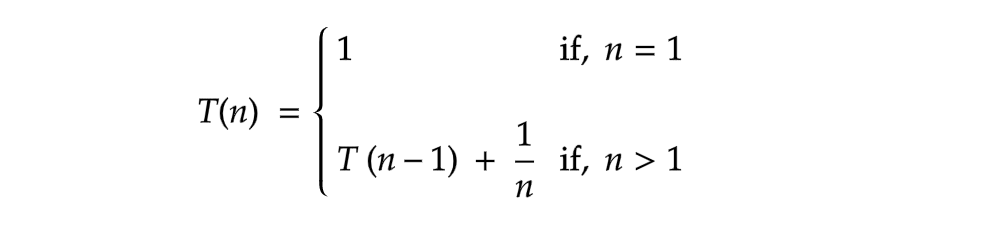You're probably wondering where this came from. We don't need to know how we got here right now. Our primary focus is on how to resolve this recurrence relation. Don't worry though, by the end of this post we will learn how to write a recurrence relation of recursive functions.

Substitution Method

Let's rewrite the equation and find the time complexity. Equation ( a )

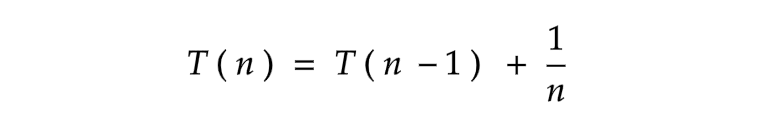
Let's find the value for T ( n - 1 ) . Before that what exactly is T ( n - 1 ) ? That is our recursive function call, where (n -1) is an argument that will eventually become a parameter. Substitute the value of T ( n ) with ( n - 1 ) . Easy right?

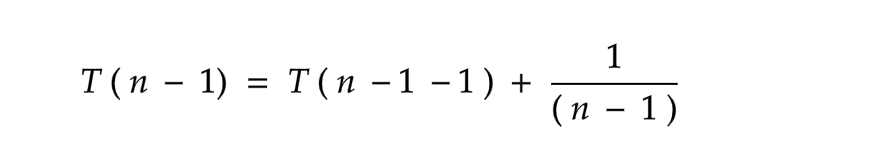
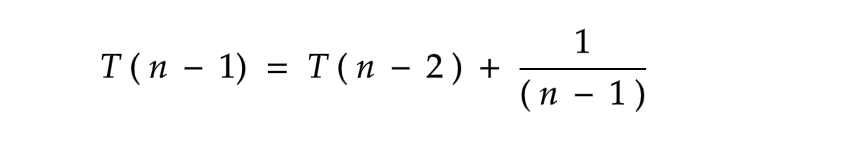
Let's see how our T ( n ) looks now by substituting this T ( n - 1 ) in equation ( a )

Equation ( b )

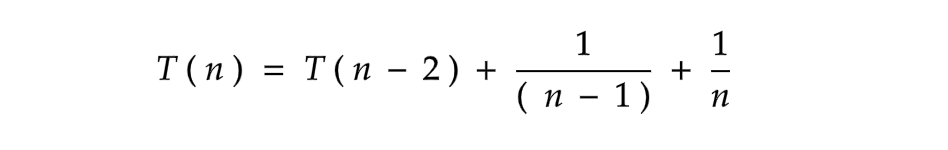You now understand, correct? It's that simple. Let's go one step further. Let's find the value of T ( n - 2 )

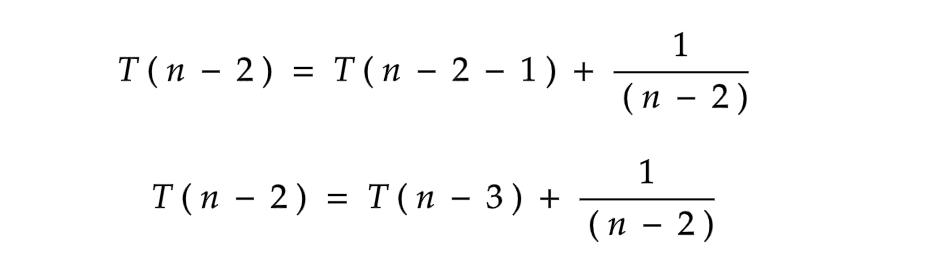
Now, if we substitute the above result for the value of T ( n - 2 ) in equation ( b ) , we get

Equation ( c )

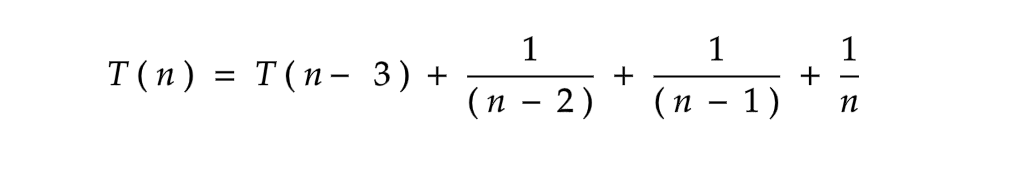
You are free to take as many steps as you desire. Assume that each reader of this article, at least one of whom has reached this line, takes any number of steps. That is, we can say it k times. As a result, the equation for k times is given below.

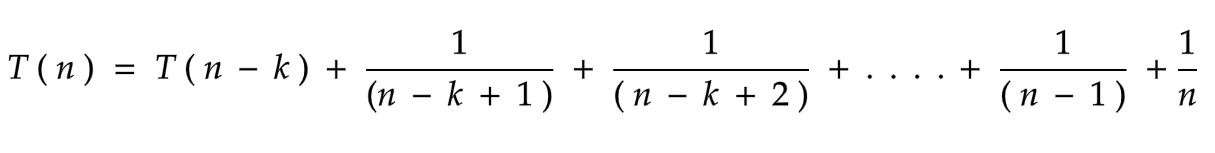In what way do we calculate ( n - k + 1 )? Substitute k for the integers in T ( n - 3 ) in equation (c) because it increases up to k times. What about ( n - 2 ), then? By applying basic reasoning, adding ( -3 + 1 ) results in the number 2. Which means ( - k + 1 ) = 2 Just that.
Now let's consider the relation

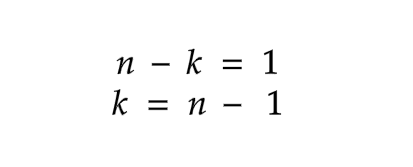Substituting the relation in the above equation.

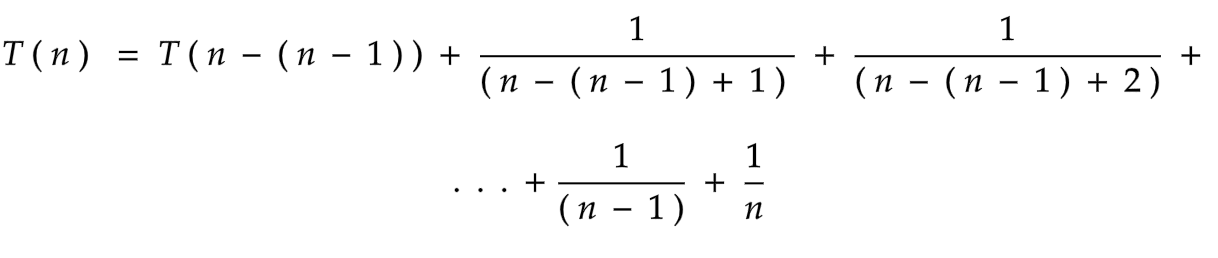
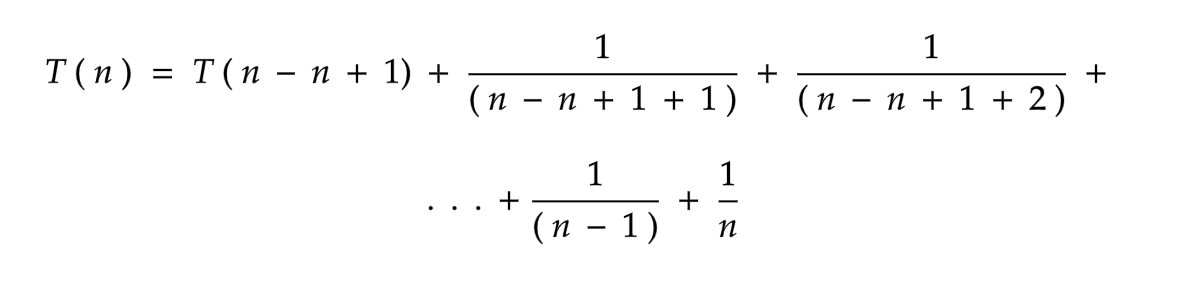
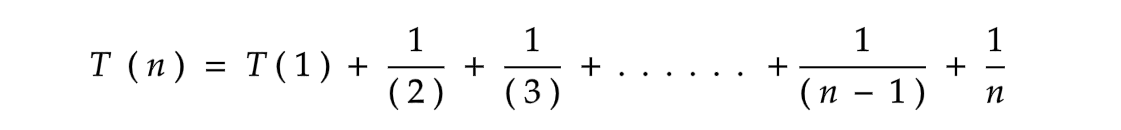
Do you remember our recurrence relation? What is the value of T ( 1 )? Let us revisit the recurrence relation once again 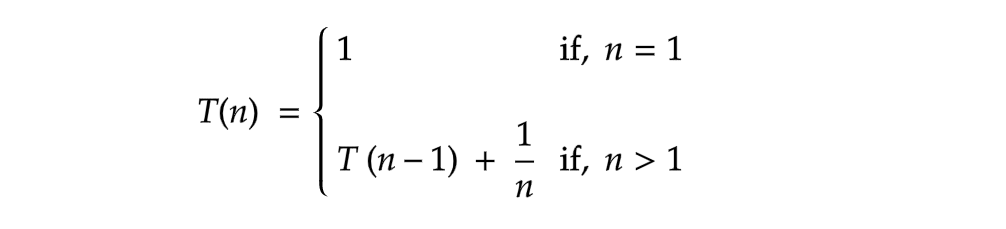When the value of n reaches 1, it returns a value of 1, which is known as the stopping condition.

So, let's apply the stopping condition and see what our final series looks like.

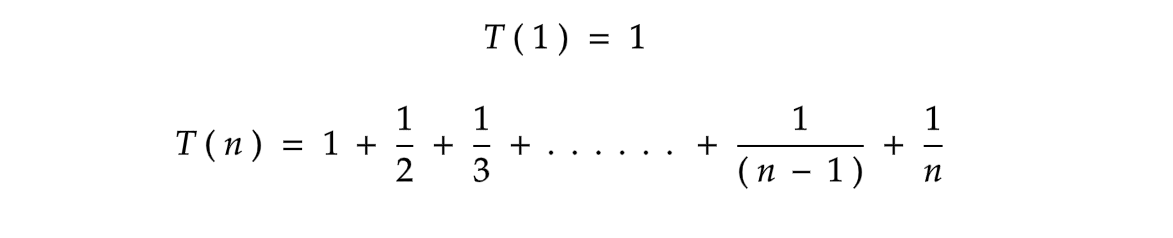So, what exactly is this series? Can you make a guess? You are correct, it is a logarithmic series. We are going to write the series as,

Time Complexity

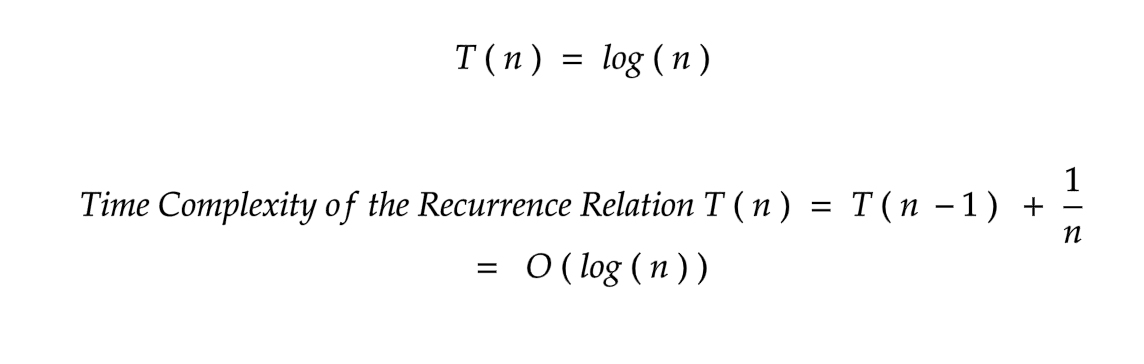
Congratulations! You've just solved a recurrence relation. But wait, we never learned how to write our own, did we? Let's look at a straightforward example of finding a number's factorial.

How do we write them on our own?

Pseudocode Example

function fact( num ){
    if( num <= 1 ) {
      return 1
    };
    return num * fact( num-1 )
}

Let's write the recurrence relation. Consider the " if " condition. What is the time complexity of carrying out that statement? Is it O ( 1 )? Because it's not in a loop. What about num fact ( num - 1 )? The num is multiplied by a function fact. So, if num = 5 , it will be multiplied 5 times until it reaches 1 because we subtract num *by 1 with each recursive call.

Let T ( n ) be a function then our equation will be

We removed the constant part because it makes no difference here.

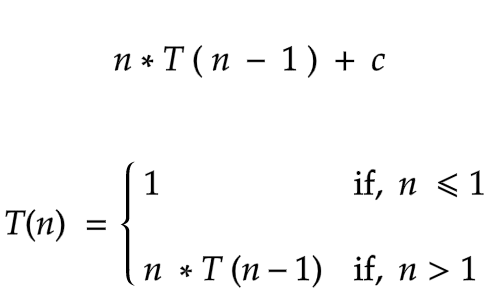
So, here is the task. Can you determine the time complexity of this recurrence relation?